Controlling voice coils with Bela

The Nyquist sampling theorem applies here. If you have a PWM resolution of 32, then the maximum frequency you can reproduce without aliasing is 689 Hz. In reality the PWM fundamental is mirrored off of every 1.38 kHz, so you technically need a brick-wall filter with 689 Hz cut-off for any of the cross-terms to go away. If you increase PWM rate but decrease resolution, then the quantization noise becomes more prominent. The extreme case is reducing resolution to 1-bit....so here is an example of a 1-bit DAC for this application.

You mentioned a noise spectral density to be more desirable/realistic anyway, so here's an example...

You can do noise shaping with a filter. I have checked in a proof-of-concept here:
https://github.com/transmogrifox/Bela_Misc/tree/master/Noise_Shaping

Rather than PWM this creates a pulse-density-modulation, which does not have a prominent peak at the PWM frequency. You can see below the harmonics of the 1 kHz filter center frequency due to the 1-bit sampling quantization noise effect.

Basically use the rand() function to get reasonably flat noise spectrum and then filter that with a biquad IIR filter (code included in case you are thinking "IIR what?".

Generating the 1-bit signal boils down to this one little function:

// Shaped noise, 1-bit sampled
// Produces prominent peak at filter cut-off
    // Gain parameter currently not implemented here
    // The implementation would be to strobe this function on
    // and off to make total output power adjustable
float randseq_tick(float gain)
{
   // Run the band-pass filter
    r_duty_f = run_filter((float) (rand()%2048)/2048.0, nf);

  //1-bit sampling:  If > 0, output is 1.0 (logic high)
// if <=0, output is 0.0 (logic low)
    if(r_duty_f > 0.0)
        return 1.0;
    else 
        return 0.0;
 
}

The rest of the code is preparing several traces of raw data and performing the FFT on it to output something I can plot in Excel.

In the end this is the spectrum you would get if you ran this algorithm sample-by-sample and output at 44.1 kHz sample rate to a digital output:

Lowering the filter Q will spread the noise spectrum more, while increasing Q will narrow it at the filter center frequency.

If you look at the Excel spreadsheet in the github repo you will see in the time domain the high-Q filtered output looks like a 1 kHz square wave. It takes a closer look to see it's a 1 kHz square wave with significant jitter.

The output with filter Q of 1.0 looks more random, but you can see there is a correlated pattern to it.

You might find in your application all you need is to output a squarewave at some frequency with integer multiples of the sampling period.

The filtered noise approach will center the peak of the noise hump right at your desired output frequency, giving you all of the in-betweens.

If you need amplitude modulation on this then you apply PWM to the 1-bit modulator output to lower its overall signal power. This will mess up your spectrum but it may be acceptable in your application. Better to do variable-frequency PWM rather than fixed frequency PWM, that is, you skip "M" pulses every "N" pulses to get gain 0.5 to 1.0. You invert this to get gain 0.0 to 0.5, e.g. you mask "M" pulses every "N" pulses.

This method lets you continuously trade off bandwidth for resolution as the signal's requirement for dynamic range increases away from 50% duty cycle.

Chosto Do you mean that there is a 1.38kHz frequency component in the output frequency spectrum - that does not exist in the input signal ? Is this because the switching frequency is fixed ?

This is correct. You would see this directly on an oscilloscope. To exactly meet the conditions of the Nyquist Sampling theorem, a brick-wall filter would be applied at 1/2 the PWM frequency and you would be left with the pure tone. In the real-world you are expecting the speaker to take off this carrier noise, but in your case the 1.38 kHz sampling period is within the band of the coil, so you either have to add steep analog filtering at the output to pull it down if it is a problem in your application.

Chosto So a 1-bit DAC is the same as PDM, but a PWM with 1-bit resolution would give nothing but a two-state analog output after being filtered by a low-pass filter ?

PDM and PWM can both be considered 1-bit DACs. PDM takes advantage of noise to evenly spread the spectral density of the quantization error over a wider frequency band. PWM focuses the quantization noise into a narrow band. You can think of PWM as putting all of the pulses of an averaging period into adjacent time slots, where PDM spreads all of those pulses at random intervals. In both cases you can increase resolution by decreasing bandwidth, even though it may initially seem counter-intuitive that you can get 16-bit resolution from a 1-bit DAC.

A 1-bit DAC like the high-end stuff uses feedback so it adjusts the average output high frequency noise power to match the low-bandwidth signal power. It's sort of like amplitude modulation where the carrier is wide-band high frequency noise. The output pulse train is filtered to remove the high frequency noise The lower frequency cut-off used, the more points used in the averaging, the higher the effective resolution. With a 44.1 kHz bit rate, you're pretty much limited to 2 or 3 bits if you want to reproduce something up to 1 kHz.

Chosto I have read that 1-bit DAC are very common nowadays, even high-end devices. Why is there a lot of quantization noise in that case ?

I think my comment above might have addressed this one too. Basically if you look at something changing between 1 and 0 at a really high rate (usually > 20 MHz) you can average it over a much longer period of time.

Say you have a sequence 10101101. Averaged over 8-samples gives you the value 0.625. As you can see this has 8-bit resolution. To change this sequence into PWM, you have 11111000, which averages to the same level. If you output this sequence repeatedly, you will get one particularly dominant frequency in the output. If you output the PDM sequence 10101101, you will get the same average value but the noise moves to a wider band at higher frequencies.

Suppose you have a sample at 0.75, 44.1 kHz base sample rate. You can output a sequence of '1' and '0' pulses that average out to 0.75 over the duration of 1/44.1k = 22.68us averaging interval. To get 16-bit resolution you need a total of 2¹⁶ pulses during that interval, so you need 44.1k*2¹⁶ 2.89GHz pulse rate -- at least, that is what you would need for PWM.

How does a sigma-delta modulator get 16-bit resolution with only a 20MHz bit rate? This is related to noise-shaping and post-filtering -- the quantization noise is pushed up into the band where it can be more easily filtered off (think of the difference between 11111000 and 10101101). It's hard for me to explain it without pointing you to a paper on sigma-delta modulators, but basically this is focusing the noise into a band that will be naturally rejected by the physical system (output filters and/or speaker).

Chosto As this is what a class D amplifier does, I think it is suited for this, am I right ?

Not the way you are thinking. A Class D pulse modulation is usually >500 kHz. You will be feeding it a 1.38 kHz square wave. The class D amp will chop that up, reconstruct it, and output an amplified version of what you put in to your speakers.

For whatever it is worth, the industry has many names for switch-mode amplifiers (like Class D). These trademark names often refer to some form of PDM/Noise Shaping as compared to classical PWM. I think some variation on PWM is still dominant in higher power amps because switching losses in the FETs would become important, lowering the efficiency of the amp. Fortunately an analog PWM circuit does not quantize the input signal so the resolution trade-off is not an issue as long as the switching frequency is high enough to be rejected by the speakers.

Chosto Also, thanks a lot for your code. I'll test it as soon as I receive the Bela.

I'm not certain my code does what you want to do. It's more of a proof-of concept regarding PDM vs PWM and the potential to spread the quantization noise. If you really want to reproduce certain wave shapes this needs to evolve into a some form of a sigma delta modulator because we can push a lot of the noise up >10 kHz.

If all you want is a variable frequency output with a noise spectrum generally centered around any arbitrary point then my code might do what you want. I'm not very familiar with haptics, nor with your particular application so I'm not sure how elegant of a system is required to do what you actually need.

I need more time to figure out what does a biquad IIR filter.

In my code it implements a band-pass function. Noise is used as the signal input, filtered noise is the signal output.

IIR stands for "infinite impulse response", which means it recirculates some of the output back to the input. Neglecting digital resolution and noise floor it would hypothetically recirculate all inputs from all time forever as the history decays toward zero. In reality the past history decays to <2^-32 (or whatever resolution) pretty quickly.

"Biquad" refers to the filter order, in this case order 2. It means the magnitude @ angle vector associated with the transfer function occupies two quadrants (phase shift limited between 0 to 180 degrees is one way to think of it). In contrast a first-order filter has phase response contained in the first quadrant (0 to 90 degrees).

What would be the effect of randomizing the digital output between 0 and 1 at 44.1kHz ?

You would essentially have something close to white noise from 0 Hz up to 44.1 kHz, rolling off above 44.1 kHz. If you want to limit to <1 kHz then you need to physically build a filter with 1 kHz cut-off for every output channel. The main disadvantage is this is time consuming and tedious.

Chosto If I understand correctly, I can generate flat noise spectrum with random values, and your approach allow to have a dominant frequency with noisy spectrum each side of the fundamental.

This sounds like you have the correct understanding. If this is seems like it will produce the desired effect then it is definitely worth a try.

Chosto Wouldn't it be with a 44.1khZ square wave if I am using PDM ?

Yes, it will be, but the Class D amp is going to be band-limited on the front-end so it will probably reject the 44.1 kHz pulses.

Anyway, I understood the issue. I need to filter the signal before amplifying it, because it will stay in range of my voice coil so it won't be filtered. I guess that I can use a LP filter before the class D amplifier to get back to an plain analog signal, but this raises the same question as before : which cut-off for PDM ?

If you are using PWM, 5-bit, then yes. If using PDM then you probably won't need an external filter. As pointed out above, the Class D amp is likely to reject the 44.1 kHz high frequency stuff but it will amplify 1.38 kHz just like any other audio-frequency stuff.

Chosto To try another formulation, PWM gives the information of the sample rate with switching frequency whereas PMD does not, so how to get this sample rate to compute average without using dark magic ?

The "dark magic" is the spectral noise shaping of the randomization algorithm used. A filter defined by the system designer sets the averaging interval (or in some cases the speaker/coil frequency response if not using an extra filter). A low-pass filter is a moving-average function and the system designer sets it to limit the output pulses to the highest frequency they want to reproduce. You can set this filter cut-off to optimize for higher bandwidth, for example, or trade bandwidth for resolution.
By example, if using PWM you will have 4-bit resolution with an equivalent output sampling rate of 1.38 kHz. With PDM you don't have the correlated 1.38 kHz output rate so the Nyquist rate for PDM is limited by the bit rate rather than the PWM period. Generating higher frequencies with PDM only means quantization noise increases but does not result in aliasing.

Chosto Why not averaging "1010" and then "1101"

Or you can set the filter cut-off for higher resolution but lower bandwidth by averaging 8 pulses rather than 4. With a PDM approach you can set the filter cut-off for bandwidth and you continuously trade resolution for bandwidth, which means that by setting filtering cut-off as a non-power-of-two ratio of the bit rate you could get something like 4.83 bit resolution (even though this makes no sense for a pure binary system). The fractional resolution represents the presence of noise.

With PWM you have to set the output sampling rate as a pre-determined fraction of the bit rate (44.1 kHz in this case).

Chosto As you said, the average for 8-bit resolution "11111000" or "10101101" is the same.

To be technically correct, this is 3-bit resolution +1 (9 unique average values). The pulse-rate in either PDM or PWM is 44.1 kHz. PWM would be a special instance of PDM in which all pulses are in adjacent time slots. Noise-shaping PDM attempts to create as many 0-1 and 1-0 transistions as possible to reduce the number of adjacent pulses.

A combination of noise-shaping (in DSP domain) and the reconstruction filter (analog domain) for a PDM DAC is really the "magic" of a sigma-delta DAC. The sigma-delta modulator pre-shapes the noise power in the quantization error, and de-correlates it so your Nyquist rate is 1/2 the bit rate rather than artificially forcing it to some lower PWM rate. Then rather than fighting against aliasing, you can continuously trade off resolution/quantization noise for bandwidth simply by picking a cut-off for the reconstruction filter.

A final note is that the special instance of PDM, that is, a sigma-delta DAC, can get higher resolution without such extreme bit rates. It's hard to explain it simply, but in short, the quantization noise is pushed up into the high frequency range, which is then easily filtered off by the reconstruction filter. I can't think of an easy intuitive way to explain this, but it has some sense in the example of comparing "11111000" output sequence to "10101101" output sequence. The sigma-delta output will have the maximum number of 1-0 transitions as possible to generate a sequence that does not repeat any patterns not directly related to the signal being modulated.

For example, if the PDM DAC was commanded to output a constant 0.625, (using the example above), you wouldn't see this:
10101101 10101101
(above space placed between the two frames to show a repeating sequence)
But something like this might be more likely:
1010110110110101
(above space removed to demonstrate there is no repeating block nor framing)
So the pair of "1's" would randomly appear in a different place. There is no consistent framing nor block size, but start at any point in the sequence and end at any point in the sequence the average will be 0.625.

I picked a number that can be represented precisely by 4 bits. For a number that does not fall directly on multiple of 1/8 would require an average of more than 8 elements in the sequence. If one attempted to represent a constant 0.677 over an averaging interval of 8 elements then it would be a noisy 0.625. This is a simple effect of needing a lot more than 4 bits to exactly represent 0.677. To average over more than 4 bits reduces the bandwidth because a low-pass filter to average over more bits naturally has a lower cut-off frequency.

Chosto Being able to do PDM for almost any signal is... wow ! I

Keep in mind this is also useful for other systems such as Arduino or any microcontroller applications where you need a lot of DAC output channels but don't need high fidelity.

Chosto I hope that my class D amp is really bandlimited on the input, because it is not said in any spec that I read.

Even if not it will just put the PDM onto the speaker and the speaker will filter it in the end.

Chosto Combining noise with the input signal (is this dithering ?) will decorrelate the quantization error

Yes, this is dithering. In a faster bit-rate system I probably would not have used this, but I think the use of dithering will be advantageous for your application.

Chosto Noise-shaping uses a feedback loop to re-inject the quantization error to the next sample. I "feel" that given the high bit rate, this will push noise power to high frequencies, but I can't really explain that.

Yes, you feel this correctly. In a true sigma-delta modulator the LPF is an integrator, which has extremely high gain at low frequencies. The average of the output pulse train will strongly suppress the error between the input and output at lower frequencies, so the noise tends to be the highest above the frequency where the integrator slope crosses 0dB.

The more true delta-sigma modulator might be worth trying...I just got going on one technique and stuck with it.

Chosto Now, the noise power is quite low in low frequencies, so we can choose any cut-off <= 1/2 the bit rate without having a peak at the cut-off frequency.

This is correct. To my ears all of the noise sounds like white noise when I listen to my demo code through speakers.

Chosto ryjobil Then look at Analysis2.ods and plots

I cannot find this file in the repository.

[EDIT] I got it added into the repo. Here's the image for faster access:

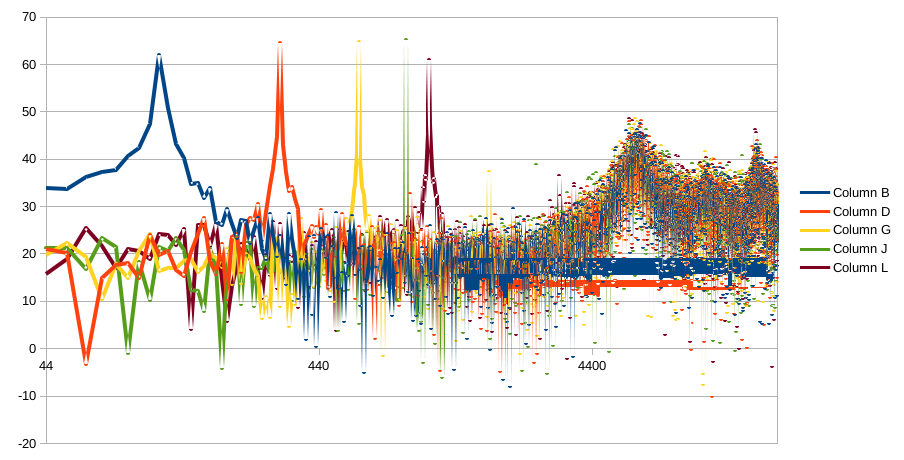
From this you can see signal peaks are >30 dB higher than the noise floor, and then the noise peak pushed up into the > 4 kHz band. If your voice coils are responsive enough around 4 kHz to make a vibration that can be felt you may need to suppress this with an RC filter at the Bela output, or push this peak higher (higher cut-off in the LPF) to take advantage of the speakers natural filtering...but then the noise floor in the low frequency range will come up.

Chosto Just a few questions :

What is the relation between lfo and pure_sine ? I am confused since in set_sine_oscillator_frequency, I can see the 2pif (angular frequency), but multiplied by Ts. Initially, f is 150Hz and Ts is 1/44.1kHz for pure_sine, but then f becomes sine_oscillator_tick(lfo)in set_sine_oscillator_frequency(pure_sine, sine_oscillator_tick(lfo));.

This part of the code is just a police siren sound. The LFO changes the frequency of the audio-frequency "pure sine" chirping up and down over the course of a few seconds. This is not part of the PDM implementation -- it's just a test signal to hear the effect in my speakers.

Also, I can see noise shaping, but just to be sure : if( (input - lpf1->y1) > 0.0) is the place where the feedback loop takes place, right ?

Yes, this is where the feedback loop takes place. The noise pre-added to the input is high-pass filtered so it has the highest noise density in the high frequency range. This noise is what de-correlates the output rate. As addressed earlier, this is dithering.

input = x + hf_noise_gen(hpf1, hpf2);

Then looking at hf_noise_gen() you see it has a 4rth order IIR high-pass applied (two cascaded 2nd order filters):

 // Noise shaped for highest density at high frequencies
return run_filter(run_filter( ((float) (rand()%65536))/65536.0, hpf1)/50.0, hpf2);

Also, is it an IIR filter because y1 is function of y1 ? Also, your always run the biquad filter twice, does this mean that the result corresponds to a higher order filter ?

Yes it is an IIR filter and you are correct it is a higher order filter because the function is run twice, but notice it is run on a second set of state variables (. It is a 2nd-order filter run on another 2nd-order filter for a total of 4-order filter.

Notice that if you simply ran the same filter twice this would not be the same thing.

Chosto ryjobil by setting filtering cut-off as a non-power-of-two ratio of the bit rate

Saved this for last. The filter cut-off corresponds roughly to the moving-averaging interval. So if you have a bit-rate of 44.1 kHz and use a moving-average with cut-off filter at (for example) 1 kHz, then the averaging interval becomes 1ms.

The number of samples averaged is 44.1 kHz * (1/1kHz) = 44.1 samples. log_2(44.1) = 5.46 Bits

Above is a simplification to communicate the idea. Remember this is an analog filter in the outside continuous-time world, so the filter will be a weighted moving average that will be the most strongly influenced by what happened in the past 1 ms, but stuff that happened beyond 1 ms will also be averaged into the output in progressively lower amounts. An integral of the impulse response would need to be computed in order to come up with an actual equivalent resolution.

In either case it is more apparent quantization error is better treated as high frequency noise that you can filter since fractional bits resolution aren't intuitive units of measure. The quantization error can be treated as a signal-noise ratio more intuitively than a fractional number of bits resolution. The lower the cut-off and the steeper the filter, the lower the noise.

Based on the premise that audio CODECS can produce 16-bit resolution @ 44.1 kHz from a 20-MHz bit rate I would surmise a 44.1 kHz bit rate could produce 16-bit signals <50 Hz with the correct PDM algorithm and analog filtering. That said you could use the digital outputs to drive a subwoofer with fairly good fidelity (but not using my noisy dithered approach -- the modulator would need to be a proper sigma-delta).